向量和标量
标量:只有大小的量。例如:一个物体距离50米。
向量:既有大小也有方向。例如:一个距离原点x方向50米,y方向20米,也就是(50,20)。
向量的模:向量的大小。
单位向量:大小为1的向量,也就是模为1的向量。例如在游戏中,如果只是想获取到一个物体的方向,这个物体可能向量很大例如(989,989),那么就可以把该向量转换为单位向量(1,1),这个过程也叫做向量的单位化或向量的归一化。
向量计算概念
加法
例如有两个向量,a = (1,2),b = (2,1),那么a + b = (3,3),向量的相加遵循平行四边形法则
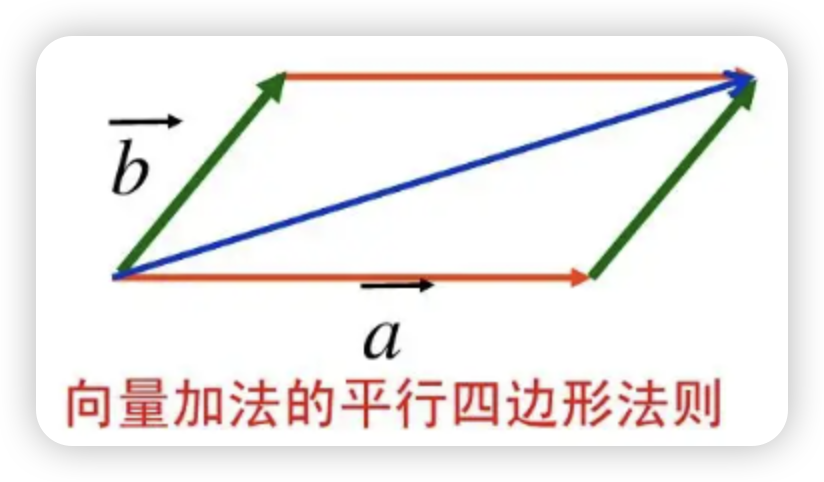
减法
例如有两个向量,a = (5,3),b = (2,1),那么a + b = (3,2),向量的相减遵循三角形法则
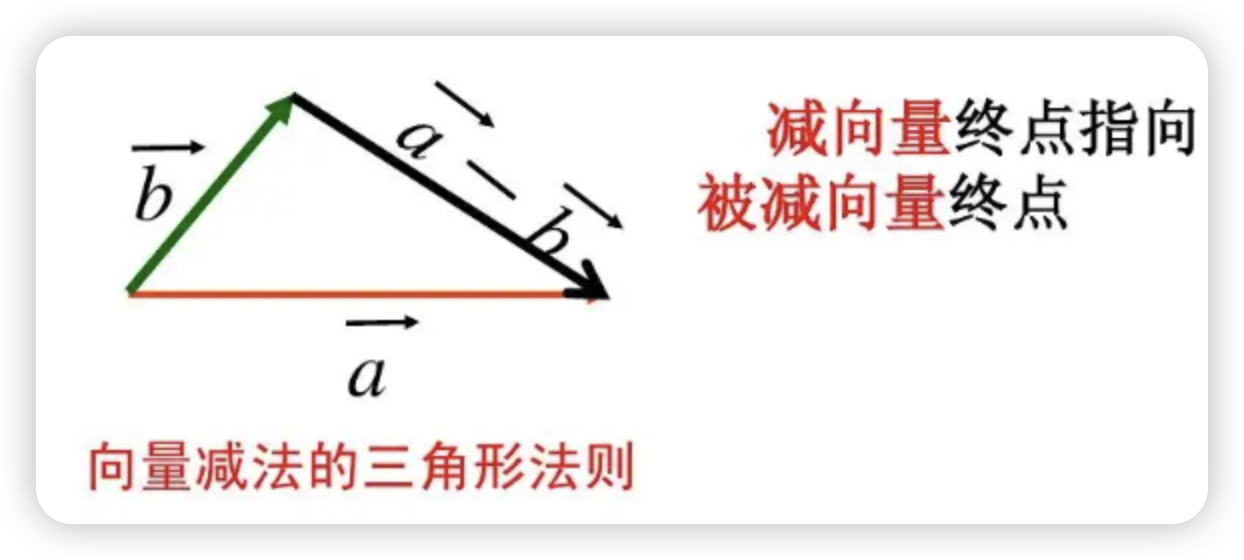
乘法
向量一般情况下和一个标量相乘,例如向量a = (1,2)和一个标量2进行相乘,得到的结果是将该向量延长,但是并不改变方向
点乘
A = (Ax,Yy),B = (Bx,By),点乘就是A·B = (Ax*Bx + Ay*By) = n,得到的结果是一个标量n。
这个标量n又有如下关系:n = |A| * |B| * Cosθ,其中|A|和|B|分别代表两个向量的模,Cosθ代表两个向量之间的夹角的Cos值。
也就是(Ax*Bx + Ay*By) = |A| * |B| * Cosθ。
由于我们只想获取两个向量的夹角,所以我们可以计算出两个向量的单位向量C和D。
由于单位向量的模为1,如此,我们就可以简化上面的公式,(Cx*Dx + Cy*Dy) = Cosθ
API
计算点乘
Vector3 right = Vector3.right; // (1,0,0)
Vector3 forward = Vector3.forward; // (0,0,1)
float angle = Vector3.Dot(forward,right);
Debug.Log(angle); // 0
计算夹角
Vector3 right = Vector3.right; // (1,0,0)
Vector3 forward = Vector3.forward; // (0,0,1)
float angle = Vector3.Angle(forward,right);
Debug.Log(angle); // 90
计算两点距离
Vector3 right = Vector3.right; // (1,0,0)
Vector3 forward = Vector3.forward; // (0,0,1)
float angle = Vector3.Distance(forward,right);
Debug.Log(angle); // 1.414214
插值
Vector3 v1 = Vector3.zero; // (0,0,0)
Vector3 v2 = Vector3.one; // (1,1,1)
Vector3 lerp = Vector3.Lerp(v1,v2,0.8f);
Debug.Log(lerp); // (0.80, 0.80, 0.80)
向量的模
Vector3 v = Vector3.one; // (1,1,1)
Debug.Log(v.magnitude); // 1.732051
归一化
Vector3 v = new Vector3(4,2,2);
Debug.Log(v.normalized); // (0.82, 0.41, 0.41)